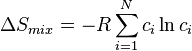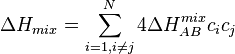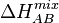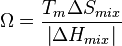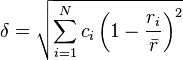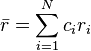Contents†
ハイエントロピー合金 (High entropy alloys) Wikipedia 英語版の簡約†
以下、Wikipedia の High Entropy Alloysの簡単な和訳です (Wikipedia ハイエントロピー合金)。
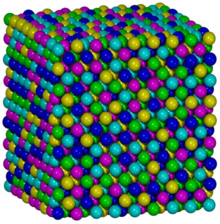
Fcc-CoCrFeMnFeハイエントロピー合金の原子模型[2]
はじめに†
High-entropy alloys (HEAs) are a class of multi-component alloys composed of 5 or more principal constituent elements each with a concentration between 5 and 35 atomic %.[1].
ハイエントロピー合金は、5元系あるいはそれよりも多成分系からなり、かつそれぞれの構成元素の組成が5~35 at.%となる合金の一つである [1]。
The defining feature of HEAs over other complex alloys is that they consist entirely or primarily of a simple solid solution phase, thus having a high entropy of mixing.
ハイエントロピー合金と他の多成分合金の異なる点は、ハイエントロピー合金は固溶体単相あるいは主相が固溶体相であり、高い混合のエントロピーを持つ点にある。
HEAs have been described in the literature that have better strength-to-weight ratios, fracture toughness, tensile strength, high-temperature strength, thermal stability,[3] or corrosion resistance than similar conventional alloys.[1][4]
ハイエントロピー合金は、一般的な合金と比べ、高い比強度、破壊靭性、高温強度、熱的安定性 [3]、耐食性などを示す[1][4]。
1. 開発の初期 (Early development)†
Although HEAs were described as early as 1996,[5] significant research interest did not develop until after independent 2004 papers by Jien-Wei Yeh and Brian Cantor, with Yeh's first paper on the topic published 2 months sooner.
ハイエントロピー合金の概念については1996年以前に提出されていたが [5]、Jien-Wei Yeh教授 と Brian Cantor教授によって2004年にそれぞれ独立に提出された論文以前には大きな関心を集めてこなかった。
Yeh also coined the term "high-entropy alloy" when he attributed the high configurational entropy as the mechanism stabilizing the solid solution phase.[6]
Yeh教授は、さらに、固溶体を安定化するメカニズムとして高い配置のエントロピーが寄与する"high-entropy alloy"という言葉をつくりだした。[6]
Cantor, not knowing of Yeh's work, did not describe his alloy as a "high-entropy alloy", but the base alloy he developed, equiatomic FeCrMnNiCo, has been the subject of considerable work in the field.[7]
Cantor教授は、Yeh教授の研究を知らず、Yeh教授の合金を"high-entropy alloy"とは呼ばなかった。しかし、Cantor教授が開発した等原子組成 FeCrMnNiCo合金は、この分野における極めて重要な研究であった。[7]
Before the classification of high entropy alloys and multi-component systems, nuclear science had highlighted a system that can now be classified a high entropy alloy: within nuclear fuels Mo-Pd-Rh-Ru-Tc particles form at grain boundaries and at fission gas bubbles.[8]
ハイエントロピー合金と多成分系合金の分類がなされる以前に、原子力材料の分野において、現在ではハイエントロピー合金に分類される合金が注目されていた:核燃料であるMo-Pd-Rh-Ru-Tc粒子が、結晶粒界や核分裂ガスバブルの部分に形成される。[8]
Understanding the behavior of these '5 metal particles' was of specific interest to the medical industry as Tc-99m is an important medical imaging isotope.
'5 金属粒子'の挙動を理解することは、医療用イメージングアイソトープとして重要であるTc-99mとして医療の分野では重要であった。
2 定義 (Definition)†
There is no universally agreed-upon definition of a HEA.
ハイエントロピー合金に関する共通の定義は無い。
Yeh originally defined HEAs as alloys containing at least 5 elements with concentrations between 5 and 35 atomic percent.[6]
Yeh教授は、ハイエントロピー合金を、「少なくとも5成分系からなり、それぞれの元素の組成が5~35at.%のもの」と定義した。[6]
Later research however, suggested that this definition could be expanded.
しかし、その後の研究によってその定義は拡張された。
Otto et al. suggested that only alloys that form a solid solution with no intermetallic phases should be considered true high-entropy alloys, as the formation of ordered phases decreases the entropy of the system.[9]
Ottoらは、規則相の形成は系のエントロピーを減少させるので、金属間化合物を含まない固溶体を形成する合金のみを真のハイエントロピー合金と考えるべきであると提案した。[9]
Some authors have described 4-component alloys as high-entropy alloys [10], while others have suggested that alloys meeting the other requirements of HEAs, but with only 2~4 elements[11] or a mixing entropy between R and 1.5R[12] should be considered "medium-entropy" alloys.[13]
いくつかの研究者は、4元系合金でもハイエントロピー合金であると述べており[10]、また別の研究者は他のハイエントピー合金の条件を提案している。しかし、2~4元系合金[11]、あるいは混合のエントロピーがR~1.5Rの間にあるもの[12]は、"medium-entropy"合金であると考えるべきである。[13]
3 合金設計 (Alloy design)†
In conventional alloy design, one primary element such as iron, copper, or aluminum is chosen for its properties.
一般的な合金設計の場合、Fe、CuあるいはAlといった主要元素がその特性に応じて選択される。
Then, small amounts of additional elements are added to improve or add properties.
この場合、少量の添加元素がmその特性改善のために添加される。
Even among binary alloy systems, there are few common cases of both elements being used in nearly-equal proportions such as Pb-Sn solders.
二元系合金の場合であっても、Pb-Snはんだ合金のような、ほぼ等原子組成の合金の数は少ない。
Therefore, much is known from experimental results about phases near the edges of binary phase diagrams and the corners of ternary phase diagrams and much less is known about phases near the centers.
したがって、二元系合金の端の部分あるいは三元系合金のコーナー部分における実験結果からこれらの合金に関する特性はよく知られている。一方、三元系合金の中央部分に関する情報は極めて少ない。
In higher-order (4+ components) systems that cannot be easily represented on a 2-dimensional phase diagram, virtually nothing is known. [7]
より多成分合金系(4元系以上)では、2次元状態図を示すことが極めて困難であり、解明されていることは僅かである。
3.1 相の形成 (Phase formation)†
Gibbs' phase rule, F=C-P+2, can be used to determine an upper bound on the number of phases that will form in an equilibrium system.
ギブスの相律によれば、 F = C-P+2 (F は自由度、C は成分の数、P は相の数)であり、これを用いて、平衡状態における相の数の上限を決定することができる。
In his 2004 paper, Cantor created a 20-component alloy containing 5 at% of Mn, Cr, Fe, Co, Ni, Cu, Ag, W, Mo, Nb, Al, Cd, Sn, Pb, Bi, Zn, Ge, Si, Sb, and Mg.
2004年、Cantor教授は、Mn, Cr, Fe, Co, Ni, Cu, Ag, W, Mo, Nb, Al, Cd, Sn, Pb, Bi, Zn, Ge, Si, Sb, および Mgが5 at%となる20成分合金を作製した。
At constant pressure, the phase rule would allow for up to 21 phases at equilibrium, but far fewer actually formed.
一定圧力であれば、この20成分系合金では平衡状態において20相の自由度をもつ。しかし、実際にはそのようなならなかった。
The predominant phase was a face-centered cubic solid solution phase, containing mainly Fe, Ni, Cr, Co, and Mn.
合金の主相はe, Ni, Cr, Co, および Mnを含むFcc固溶体相であった。
From that result, the FeCrMnNiCo alloy, which forms only a solid solution phase, was developed.[7]
これらの結果から、単相固溶体が形成されるFeCrMnNiCo合金が開発された。[7]
The Hume-Rothery rules have historically been applied to determine whether a mixture will form a solid solution.
ヒュームロザリー則は、合金の固溶体形成の指針としてこれまで用いられてきた。
Research into high-entropy alloys has found that in multi-component systems, these rules tend to be relaxed slightly.
ハイエントロピ―合金の研究において、多成分系におけるそのルールは少しゆるくなる傾向にある。
In particular, the rule that solvent and solute elements must have the same crystal structure does not seem to apply, as Fe, Ni, Cr, Co, and Mn have 4 different crystal structures as pure elements (and when the elements are present in equal concentrations, there can be no meaningful distinction between "solvent" and "solute" elements).[9]
特に、溶質と溶媒元素の結晶構造が同じであるというルールは適用できないようである。例えば、Fe, Ni, Cr, Co, および Mnでは、純物質の結晶構造は4つの異なるタイプである。(さらに、等原子組成の場合、「溶質」と「溶媒」の定義は意味をなさない。)[9]
3.2 熱力学的メカニズム (Thermodynamic mechanisms)†
The multi-component alloys Yeh developed also consisted mostly or entirely of solid solution phases, contrary to what had been expected from earlier work in multi-component systems, primarily in the field of metallic glasses.[6][14]
Yeh教授によって開発された固溶体相となる多成分合金は、これまでの多成分系合金における研究、特に金属ガラスの分野とは異なっている。[6][14]
Yeh attributed this result to the high configurational, or mixing, entropy of a random solid solution containing numerous elements.
Yeh教授は、この結果は、多成分ランダム固溶体の高い配置あるいは混合のエントロピーによるものであると考えた。
Because ΔG=ΔH-TΔS and the phase with the lowest Gibbs free energy of formation (ΔG) will be the phase formed at equilibrium, increasing ΔS (entropy) will increase the likelihood of a phase being stable.
なぜなら、次の理由からである。ギブスの自由エネルギー (ΔG) はΔG=ΔH-TΔS で与えられ、ΔGが最小となる相が平衡状態で形成される。ΔS(エントロピー)が増加は、このこのランダムな固溶体相が安定化すると考えられる。
The mixing entropy for a random ideal solid solution can be calculated by:
ランダムな理想溶体の混合のエントロピーは次式で与えられる:
where R is the ideal gas constant, N is the number of components, and ci is the atomic fraction of component i.
ここで、Rはガス定数、Nは成分の数、ciは成分iの割合である。
From this it can be seen that alloys in which the components are present in equal proportions will have the highest entropy, and adding additional elements will increase the entropy.
この式から明らかなように、等原子組成の合金で最もエントロピーが高くなり、成分数の増加とともにエントロピーが増加する。
A 5 component, equiatomic alloy will have a mixing entropy of 1.61R.[6][15]
5成分系では、等原子組成合金において混合のエントロピーは1.6Rとなる。[6][15]
However entropy alone is not sufficient to stabilize the solid solution phase in every system.
しかし、エントロピーの項だけでは、すべての系において固溶体相を安定化することはできない。
The enthalpy of mixing (ΔH), must also be taken into account.
混合のエンタルピー (ΔH)も考慮に入れなければならない。
This can be calculated using:
混合のエンタルピー (ΔH)は次式で計算される:
where
ここで、
is the binary enthalpy of mixing for A and B.[16]
は、AとBからなる二元系合金のエントロピーである。[16]
Zhang et al. found, empirically, that in order to form a complete solid solution, ΔHmix should be between -10 and 5 kJ/mol.[15]
Zhangらは、経験的に、固溶体相単相が形成されるためには、ΔHmix の値が-10 から 5 kJ/molの値である傾向を見出した。
In addition, Otto et al. found that if the alloy contains any pair of elements that tend to form ordered compounds in their binary system, a multi-component alloy containing them is also likely to form ordered compounds.[9]
さらに、Ottoらは、二成分系において規則化合物を形成する傾向にある合金があるとき、、それらのペアを含む多成分系合金においても規則構造を形成する傾向があることを見出した。[9]
Both of the thermodynamic parameters can be combined into a single, unitless parameter Ω:
エントロピー項とエンタルピー項をあわせた、無次元パラメーターΩは、下記で与えられる:
here Tm is the average melting point of the elements in the alloy.
ここで、Tmは合金中の各元素の融点の平均値である。
Ω should be greater than or equal to 1.1 to promote solid solution development.[4]
Ωが1.1あるいはそれ以上の合金で、固溶体の形成が促進される。
3.3 速度論的メカニズム (Kinetic mechanisms)†
The atomic radii of the components must also be similar in order to form a solid solution.
固溶体相を形成するためには、構成元素の原子半径が近いものである必要もある。
Zhang et al. proposed a parameter δ representing the difference in atomic radii:
Zhangらは、原子半径の違いを表すパラメーター δ を提案した。
where ri is the atomic radius of element i.
ここで、riは成分iの原子半径である。
and
さらに
Formation of a solid solution phase requires a δ≤6.6%, but some alloys with 4%<δ≤6.6% do form intermetallics.[4][15]
固溶体の形成にはδ≤6.6%が必要である。しかし、いくつか合金では、 4%<δ≤6.6%の場合に金属間化合物が形成する。[4][15]
3.4 その他の特徴 (Other properties)†
For those alloys that do form solid solutions, an additional empirical parameter has been proposed to predict the crystal structure that will form.
固溶体を形成するこれらの合金について、結晶構造を予測する別の実験的パラメーターが提案されている。
If the average valence electron concentration (VEC) of the alloy is ≥8, the alloy will form a face-centered cubic (fcc) lattice.
合金の平均価電子密度(VEC)が ≧ 8 の合金では、fcc構造が形成される。
If the average VEC is <6.87, it will form a body-centered cubic (bcc) lattice.
価電子密度(VEC)が < 6.87 の合金では、bcc構造が形成される。
For values in between, it will form a mixture of fcc and bcc.[17]
この間にある場合、fccとbccの混相となる。
VEC has also been used to predict the formation of σ-phase intermetallics (which are generally brittle and undesirable) in chromium and vanadium-containing HEAs.[18]
価電子密度(VEC)は、CrやVを含むハイエントピ―合金におけるσ相(一般的に脆く、形成が好まれない金属間化合物)の形成の予測にも用いられる。
Empirical parameters and design guidelines for forming solid solution HEAs
固溶体ハイエントロピ―合金を形成するための経験的パラメーター
| パラメーター | 固溶体形成のガイドライン |
| ∆Smix | 最大 |
| ∆Hmix | > -10 かつ < 5 kJ/mol |
| Ω | ≥ 1.1 |
| δ | ≤ 6.6% |
| VEC | ≥ 8 for fcc, <6.87 for bcc |
4 作製 (Synthesis)†
High-entropy alloys are mostly produced using distinct methods that depend on the initial phase - starting either from a liquid, solid, or gas state.
ハイエントロピー合金は、大きく異なる様々なプロセスにより作製される。プロセスは、初期原料の相、すなわち液体、気体、あるいは固体状態のどの状態から作製されるかによって異なる。
Most HEAs have been produced using liquid-phase methods include arc melting, induction melting, and Bridgman solidification.[4]
多くのハイエントrピー合金は、アーク溶解法、高周波溶解法、ブリッジマン法など、液体状態から作製される。[4]
Solid-state processing is generally done by mechanical alloying using a high-energy ball mill.
固体プロセスとしては、高エネルギーボールミリングを用いたメカニカルアロイングが一般的に用いられる。
This method produces powders that can then be processed using conventional powder metallurgy methods or spark plasma sintering.
メカニカルアロイングにより、一般的な粉末焼結法あるいはスパークプラズマ焼結法(SPS法)に用いられる粉末が得られる。
This method allows for alloys to be produced that would be difficult or impossible to produce using casting, such as AlLiMgScTi, in which the melting points of the constituent elements has a range of nearly 1500 °C.[4][19][20]
この手法は、鋳造法の適用が困難あるいは不可能な合金系、例えば、構成元素の融点の範囲が1500℃に及ぶようなAlLiMgScTi合金でも、適用可能である。[4][19][20]
Gas-phase processing includes processes such as sputtering or molecular beam epitaxy (MBE), which can be used to carefully control different elemental compositions to get high-entropy metallic[3] or ceramic films.[4]
気相法は、スパッタリングや分子線エピタキシー法(MBE法)などのプロセスであり、異なる元素組成を注意深くコントロールすることで、ハイエントロピー合金[3]あるいはセラミックス[4]を得ることができる。
Other HEAs have been produced by thermal spray, laser cladding, and electrodeposition.[4][21]
他の手法として、溶射法、レーザークラッディング法、電析法などがある。[4][21]
5 モデリングとシミュレーション (Modeling and simulation)†
The atomic-scale complexity presents additional challenges to computational modelling of high-entropy alloys.
原子スケールの複雑さは、ハイエントロピー合金における計算機モデリングの課題となっている。
Thermodynamic modelling using the CALPHAD method requires extrapolating from binary and ternary systems.[22]
CALPHAD法を用いる熱力学モデリングにおいては、二元系および三元系からの拡張が必要である。[22]
Most commercial thermodynamic databases are designed for, and may only be valid for, alloys consisting primarily of a single element.
ほとんどの商用熱力学データベースは、一つの元素を主要元素とする合金用にデザインされている。
Thus, they require experimental verification or additional ab initio calculations such as density functional theory (DFT).[23]
したがって、実験的検証あるいは密度汎関数理論(DFT)などの非経験的計算法を用いた追加の計算が必要となる。
However, DFT modeling of complex, random alloys has its own challenges, as the method requires defining a fixed-size cell, which can introduce non-random periodicity.
しかし、複雑な、ランダム構造合金のDFTモデリングは極めて困難である。これは、DFTモデリングにおける大きさの決まったセルの定義の必要性は、ランダムではない周期性をもつ材料の計算という制約があるためである。
This is commonly overcome using the method of "special quasirandom structures," designed to most closely approximate the radial distribution function of a random system,[24] combined with the Vienna Ab-initio Simulation Package.
この問題は、一般に "special quasirandom structures (SQS)" 法を用いて解決される。SQSは、ランダムな系における動径分布関数を最も正確に近似するようにデザインされた方法であり、Vienna Ab-initio Simulation Package(VASP)と連動している。
Using this method, it has been shown that results of a 4-component equiatomic alloy begins to converge with a cell as small as 24 atoms.[25][26]
この方法を用いて、24原子を含むセルを用いた4成分等原子組成合金の計算結果が示された。[25][26]
The exact muffin-tin orbital method with the coherent potential approximation has also been employed to model HEAs.[25][27]
コヒーレントポテンシャル近似を用いた正確なマフィンティンポテンシャル軌道計算が、ハイエントロピー合金のモデル化に適用された。[25][27]
Other techniques include the 'multiple randomly populated supercell' approach, which better describes the random population of a true solid solution (although is far more computationally demanding).[28]
真の固溶体におけるランダムな分布をより記述可能な、'multiple randomly populated supercell'を含む他の手法も試みられた。
This method has also been used to model glassy/amorphous (including bulk metallic glasses) systems without a crystal lattice.[29][30]
この手法は、結晶構造以外にも、(バルク金属ガラスを含む)ガラス/アモルファス材料のモデル化にも用いられてきた。
Further, modeling techniques are being used to suggest new HEAs for targeted applications.
さらに、モデリング手法は、応用を念頭においた新しいハイエントロピー合金の提案にも用いられる。
The use of modeling techniques in this 'combinatorial explosion' is necessary for targeted and rapid HEA discovery and application.
この'combinatorial explosion'は、ハイエントロピー合金の迅速な開発や応用に必要である。
Simulations have highlighted the preference for local ordering in some high entropy alloys.
シミュレーションは、いくつかのハイエントロピー合金の局所的な規則性を強調した。
And, when the enthalpies of formation are combined with terms for configurational entropy, transition temperatures between order and disorder can be estimated.[31] - allowing one to understand when effects like age hardening and degradation of an alloy's mechanical properties may be an issue.
さらに、形成のエンタルピーと配置のエントロピーを組み合わせ、規則-不規則温度が見積もられている[31]-時効効果や機械的性質の劣化などにおよぼす合金化の影響に知見を与えるかもしれない。
6 特徴と実用化の可能性 (Properties and potential uses)†
6.1 機械的性質 (Mechanical)†
The crystal structure of HEAs has been found to be the dominant factor in determining the mechanical properties.
ハイエントロピー合金の結晶構造は、この合金の機械的性質の重要な因子であることが見いだされている。
Bcc HEAs typically have high yield strength and low ductility and vice versa for fcc HEAs.
一般的に、Bcc構造ハイエントロピー合金は高強度で延性が低い。一方、fcc構造ハイエントロピー合金はその逆で、強度は低いが高延性である。
Some alloys have been particularly noted for their exceptional mechanical properties.
いくつかの合金系については、部分的にではあるが、卓越した機械的性質を示すことが報告されている。
A refractory alloy, VNbMoTaW maintains a high yield strength (>600 MPa (87 ksi)) even at a temperature of 1,400 °C (2,550 °F), significantly outperforming conventional superalloys such as Inconel 718.
耐熱合金である、VNbMoTaWハイエントロピー合金は、1400℃においても極めて高い降伏強度 (>600 MPa (87 ksi))を示し、この特性はInconel 718といった一般的な超合金を上回る特性を示す。
However, room temperature ductility is poor, less is known about other important high temperature properties such as creep resistance, and the density of the alloy is higher than conventional nickel-based superalloys.[4]
しかし、室温延性は乏しく、クリープといったその他の重要な高温特性については解明されておらず、またその密度は一般的なNi基超合金よりも大きい。[4]
CoCrFeMnNi has been found to have exceptional low-temperature mechanical properties and high fracture toughness, with both ductility and yield strength increasing as the test temperature was reduced from room temperature to 77 K (?321.1 °F).
CoCrFeMnNiハイエントロピー合金は、卓越した低温度での機械的性質と高い破壊靭性を示すことが見いだされている。低温度特性として、延性と降伏強度は、室温から77 K (?321.1 °F)と温度低下とともに増加する。
This was attributed to the onset of nanoscale twin boundary formation, an additional deformation mechanism that was not in effect at higher temperatures.
これはナノスケール双晶境界の形成によるものであり、高温度域にはない新たな変形メカニズムによるものである。
As such, it may have applications as a structural material in low-temperature applications or, because of its high toughness, as an energy-absorbing material.[32]
したがって、CoCrFeMnNiハイエントロピー合金は、その強靱性を利用して、エネルギー吸収材料などの低温度構造材としての適用の可能性がある。
However, later research showed that lower-entropy alloys with fewer elements or non-equiatomic compositions may have higher strength[33] or higher toughness.[34]
しかし、その後の研究は、少量の添加元素を含むあるいは等原子組成から少しずれた低エントロピー合金のほうが、高強度[33]や高靭性[34]を示す可能性があることを示唆した。
No ductile to brittle transition was observed in the bcc AlCoCrFeNi alloy in tests as low as 77 K.[4]
Bcc構造AlCoCrFeNiハイエントロピー合金は、延性-脆性転移温度を示さない[4]。
Al0.5CoCrCuFeNi was found to have a high fatigue life and endurance limit, possibly exceeding some conventional steel and titanium alloys.
Al0.5CoCrCuFeNiハイエントロピー合金は、高い疲労寿命と耐久限界を示すことが見いだされており、その特性は汎用の鋼やチタン合金を上回る可能性がある。
But there was significant variability in the results, suggesting the material is very sensitve to defects introduced during manufacturing such as aluminum oxide particles and microcracks.[35]
しかし、実験結果には大きなバラつきがある。これは、合金の疲労特性が、アルミ酸化物やマイクロクラックといった試料作製中に混入した介在物に敏感であることを示している。
A single-phase nanocrystalline Al20Li20Mg10Sc20Ti30 alloy was developed with a density of 2.67 gcm-3 and microhardness of 4.9 ~ 5.8 GPa, which would give it an estimated strength-to-weight ratio comparable to ceramic materials such as silicon carbide,[19] though the high cost of scandium limits the possible uses.[36]
単相ナノ結晶Al20Li20Mg10Sc20Ti30合金は、密度が2.67 gcm-3でマイクロ硬さが4.9 ~ 5.8 GPaであり、Scを用いることによる高コストがその利用を制限するものの、シリコンカーバイドのようなセラミックス材料と同程度の比強度を持つ可能性がある。[36]
Rather than bulk HEAs, small-scale HEA samples (e.g. NbTaMoW micro-pillars) exhibit extraordinarily high yield strengths of 4-10 GPa -one order of magnitude higher than that of its bulk form- and their ductility is considerably improved.
バルクのハイエントロピー合金にl比べ、小さなスケールのハイエントロピー合金試料(すなわち NbTaMoW マイクロピラー)も4-10 GPaという極めて高い降伏強度を示す。この値は、バルク形状の値より一桁高く、またその延性も改善される。
Additionally, such HEA films show substantially enhanced stability for high-temperature, long-duration conditions (at 1,100 ?°C for 3 days).
さらに、ハイエントピ―合金薄膜は、熱的安定性が高められる。(高温で長時間安定、1100℃で3日間)
Small-scale HEAs combining these properties represent a new class of materials in small-dimension devices potentially for high-stress and high-temperature applications.[3][37]
卓越した機械的特性と熱的安定性を併せ持つ微小スケールハイエントロピー合金は、高応力-高温下で利用される微小デバイス用の新材料としての可能性を秘めている。
6.2 電気的および磁気的性質 (Electrical and magnetic)†
CoCrCuFeNi is an fcc alloy that was found to be paramagnetic.
Fcc構造CoCrCuFeNi合金は常磁性を示す。
But upon adding titanium, it forms a complex microstructure consisting of fcc solid solution, amorphous regions and nanoparticles of Laves phase, resulting in superparamagnetic behavior.[38]
しかし、Tiを添加すると、fcc固溶体、アモルファス相、およびナノスケールLaves相を含む組織となり、超常磁性を示す。[38]
High magnetic coercivity has been measured in a BiFeCoNiMn alloy [21]
BiFeCoNiMn合金において、高い磁気保磁力が測定されている。[21]
6.3 その他 (Other)†
The high concentrations of multiple elements leads to slow diffusion.
高い多成分元素濃度は、構成元素の拡散係数を低下させる。
The activation energy for diffusion was found to be higher for several elements in CoCrFeMnNi than in pure metals and stainless steels, leading to lower diffusion coefficients.[39]
CoCrFeMnNiハイエントピー合金のいくつかの元素の拡散の活性化エネルギーは、純金属やステンレス鋼に比べて高いことが見いだされており、低い拡散係数の原因となっている。
7 参考文献 (References)†
- M.H. Tsai, J.-W. Yeh, "High-Entropy Alloys: A Critical Review", Materials Research Letters 2, 107-123 (2014)., http://dx.doi.org/10.1080/21663831.2014.912690
- S. Wang, Shaoqing, Entropy 15, 5536-5548 (2013), "Atomic Structure Modeling of Multi-Principal-Element Alloys by the Principle of Maximum Entropy"., http://dx.doi.org/10.3390/e15125536
- Y. Zou, H. Ma, R. Spolenak, Nature Communications 6, 7748 (2015)., "Ultrastrong ductile and stable high-entropy alloys at small scales", http://dx.doi.org/10.1038/ncomms8748
- Y. Zhang, T. T. Zuo, Z. Tang, M. C. Gao, K. A. Dahmen, P. K. Liaw, Z. P. Lu, Progress in Materials Science 61, 1-93 (2014)., "Microstructures and properties of high-entropy alloys", http://dx.doi.org/10.1016/j.pmatsci.2013.10.001
- K.H. Huang, J.W Yeh, "A study on multicomponent alloy systems containing equal-mole elements" [M.S. thesis]. Hsinchu: National Tsing Hua University; 1996.
- J.-W. Yeh, S.-K. Chen, S.-J. Lin, J.-Y. Gan, T.-S. Chin, T.-T. Shun, C.-H. Tsau, S.-Y. Chang, Advanced Engineering Materials 6, 299-303. (2004)., "Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes"., http://dx.doi.org/10.1002/adem.200300567
- B. Cantor, I.T.H. Chang, P. Knight, A.J.B. Vincent, Materials Science and Engineering, A. 375-377, 213-218 (2004)., "Microstructural development in equiatomic multicomponent alloys"., http://dx.doi.org/10.1016/j.msea.2003.10.257.
- S.C. Middleburgh, D.M. King, G.R. Lumpkin, Royal Society Open Science 2, 140292 (2015). "Atomic scale modelling of hexagonal structured metallic fission product alloys"., http://dx.doi.org/10.1098/rsos.140292
- F. Otto, Y. Yang, H. Bei, E.P. George, Acta Materialia 61, 2628-2638 (2013)., "Relative effects of enthalpy and entropy on the phase stability of equiatomic high-entropy alloys", http://dx.doi.org/10.1016/j.actamat.2013.01.042.
- Y. Zou, S. Maiti, W. Steurer, R. Spolenak, Acta Materialia 65, 85-97 (2014), "Size-dependent plasticity in an Nb25Mo25Ta25W25 refractory high-entropy alloy", http://dx.doi.org/j.actamat.2013.11.049.
- A. Gali, E.P. George, E.P. Intermetallics 39, 74-78 (2013)., "Tensile properties of high- and medium-entropy alloys"., http://dx.doi.org/10.1016/j.intermet.2013.03.018.
- D. Miracle, J. Miller, O. Senkov, C. Woodward, M. Uchic, J. Tiley, Entropy 16, 494-525 (2014), "Exploration and Development of High-Entropy Alloys for Structural Applications", http://dx.doi.org/10.3390/e16010494.
- A. Gali, E.P. George, Intermetallics 39, 74-78 (2013)., "Tensile properties of high- and medium-entropy alloys"., http://dx.doi.org/10.1016/j.intermet.2013.03.018.
- A. Lindsay Greer, Nature 366, 303-304 (1993), "Confusion by design", http://dx.doi.org/10.1038/366303a0
- Y. Zhang, Y. J. Zhou, J.-P. Lin, G.-L. Chen, P.-K. Liaw, "Solid-Solution Phase Formation Rules for Multi-component Alloys", Advanced Engineering Materials, 10 , 534-538 (2008). http://dx.doi.org/10.1002/adem.200700240
- A. Takeuchi,A. Inoue, Akihisa, Materials Transactions 46, 2817-2829 (2005).,
"Classification of Bulk Metallic Glasses by Atomic Size Difference, Heat of Mixing and Period of Constituent Elements and Its Application to Characterization of the Main Alloying Element", http://dx.doi.org/10.2320/matertrans.46.2817
- S. Guo, C. Ng, J. Lu, C. T. Liu, Journal of Applied Physics 109, 103505 (2011)., "Effect of valence electron concentration on stability of fcc or bcc phase in high-entropy alloys", http://dx.doi.org/10.1063/1.3587228
- M.-H. Tsai, K.-Y. Tsai,C.-W. Tsai, C. Lee, C.-C. Juan, J.-W. Yeh, Materials Research Letters 1, 207-212 (2013), "Criterion for Sigma Phase Formation in Cr- and V-Containing High-Entropy Alloys", http://dx.doi.org/10.1080/21663831.2013.831382
- K. M. Youssef, A.-J. Zaddach, C. Niu, D. L. Irving, C. C. Koch, Materials Research Letters 3, 95-99 (2014)., "A Novel Low-Density, High-Hardness, High-entropy Alloy with Close-packed Single-phase Nanocrystalline Structures", http://dx.doi.org/10.1080/21663831.2014.985855
- W. Ji, W. Wang, Weimin, H. Wang, Z. Hao, J. Zhang, Y. Wang, F. Zhang, Fan; Z. Fu, Intermetallics 56, 24-27 (2015), "Alloying behavior and novel properties of CoCrFeNiMn high-entropy alloy fabricated by mechanical alloying and spark plasma sintering", http://dx.doi.org/10.1016/j.intermet.2014.08.008
- C.-Z. Yao, P. Zhang, M. Liu, G.-R. Li, J.-Q. Ye, P. Liu, Y.-X. Tong, Electrochimica Acta 53, 8359-8365 (2008), "Electrochemical preparation and magnetic study of Bi-Fe-Co-Ni-Mn high-entropy alloy", http://dx.doi.org/10.1016/j.electacta.2008.06.036
- C. Zhang, F. Zhang,S. Chen, W. Cao, JOM 64, 839-845 (2012), "Computational Thermodynamics Aided High-Entropy Alloy Design", http://dx.doi.org/10.1007/s11837-012-0365-6
- M. C. Gao, D. E. Alman, Entropy 15, 4504-4519 (2013), "Searching for Next Single-Phase High-Entropy Alloy Compositions", http://dx.doi.org/10.3390/e15104504
- A. Zunger, S.-H. Wei, L. G. Ferreira, J. E. Bernard, Physical Review Letters 65 , 353-356 (1990), "Special quasirandom structures", http://dx.doi.org/10.1103/PhysRevLett.65.353
- C. Niu, A. J. Zaddach, A. A. Oni, X. Sang, J. W. Hurt III, J. M. LeBeau, C. C. Koch, D. L. Irving, Applied Physics Letters 106, 161906 (2015), "Spin-driven ordering of Cr in the equiatomic high-entropy alloy NiFeCrCo", http://dx.doi.org/10.1063/1.4918996
- W. P. Huhn, M. Widom, JOM 65, 1772-1779 (2013), "Prediction of A2 to B2 Phase Transition in the High-Entropy Alloy Mo-Nb-Ta-W", http://dx.doi.org/10.1007/s11837-013-0772-3
- F. Tian, L. Delczeg, N. Chen, L. K. Varga, J. Shen, L. Vitos, Physical Review B 88, 085128 (2013), "Structural stability of NiCoFeCrAl high-entropy alloy from ab initio theory", http://dx.doi.org/10.1103/PhysRevB.88.085128
- S.C. Middleburgh, D.M. King, G.R. Lumpkin, M. Cortie, L. Edwards, Journal of Alloys and Compounds, 599, 179-182 (2014), "Segregation and migration of species in the CrCoFeNi high entropy alloy", http://dx.doi.org/10.1016/j.jallcom.2014.01.135
- D.J.M. King, S.C. Middleburgh, A.C.Y. Liu, H.A. Tahini, G.R. Lumpkin, M.B. Cortie, Acta Materialia 83, 269-275 (2014)., "Formation and structure of V?Zr amorphous alloy thin films", http://dx.doi.org/10.1016/j.actamat.2014.10.016
- S.C. Middleburgh, P.A. Burr, D.J.M. King, L. Edwards, G.R. Lumpkin, R.W. Grimes, Journal of Nuclear Materials 466, 739-744 (2015)., "Structural stability and fission product behaviour in U3Si", http://dx.doi.org/10.1016/j.jnucmat.2015.04.052
- D. M. King, S. C. Middleburgh, L. Edwards, G. R. Lumpkin, M. Cortie, JOM, 67, 2375-2380 (2015), "Predicting the Crystal Structure and Phase Transitions in High-Entropy Alloys", http://dx.doi.org/10.1007/s11837-015-1495-4
- F. Otto, A. Dlouhy, Ch. Somsen, H. Bei, G. Eggeler, E.P. George, Acta Materialia 61, 5743-5755 (2013), "The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy", http://dx.doi.org/10.1016/j.actamat.2013.06.018
- Z. Wu, H. Bei, F. Otto, G.M. Pharr, E.P. George, Intermetallics 46, 131-140 (2014)., "Recovery, recrystallization, grain growth and phase stability of a family of FCC-structured multi-component equiatomic solid solution alloys", http://dx.doi.org/10.1016/j.intermet.2013.10.024
- A.J. Zaddach, R.O. Scattergood, C.C. Koch, Materials Science and Engineering: A 636, 373-378 (2015), "Tensile properties of low-stacking fault energy high-entropy alloys", http://dx.doi.org/10.1016/j.msea.2015.03.109
- M.A. Hemphill, T. Yuan, G.Y. Wang, J.W. Yeh, C.W. Tsai, A. Chuang, P.K. Liaw, Acta Materialia 60, 5723-5734 (2012), "Fatigue behavior of Al0.5CoCrCuFeNi high-entropy alloys", http://dx.doi.org/10.1016/j.actamat.2012.06.046
- M. Shipman, "New 'high-entropy' alloy is as light as aluminum, as strong as titanium alloys". Phys. org. Retrieved 29 May 2015., http://phys.org/news/2014-12-high-entropy-alloy-aluminum-strong-titanium.html
- Yu Zou, Soumyadipta Maiti, Walter Steurer, Ralph Spolenak, Intermetallics 15, 357-362 (2014), "Size-dependent plasticity in an Nb25Mo25Ta25W25 refractory high-entropy alloy", http://dx.doi.org/10.1016/j.actamat.2013.11.049
- X.F. Wang, Y. Zhang, Y. Qiao, G.L. Chen, Intermetallics, 15, 357-362 (2007), "Novel microstructure and properties of multicomponent CoCrCuFeNiTix alloys, http://dx.doi.org/10.1016/j.intermet.2006.08.005
- K.-Y. Tsai, M.-H. Tsai, J.-W. Yeh, Acta Materialia 61, 4887-4897 (2013), "Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys", http://dx.doi.org/10.1016/j.actamat.2013.04.058
これは、Wikipedia の High Entropy Alloys (https://en.wikipedia.org/wiki/High_entropy_alloys)の簡単な和訳です。
![[PukiWiki] [PukiWiki]](image/01.png) Top/ハイエントロピー合金
Top/ハイエントロピー合金
![[PukiWiki] [PukiWiki]](image/01.png) Top/ハイエントロピー合金
Top/ハイエントロピー合金